teaser mediathek

Data Preparation Package

The Data Preparation Package (DPP) is a software package for the regression of thermophysical property models. Using a plugin interface any kind of thermodynamic model could be used for the calculation of thermophysical properties.

The DECHEMA Data Preparation Package (DPP) is part of the DETHERM Software Suite. It closes the gap between raw thermophysical data and model based process simulation packages. It allows

  • selection und graphical display of data sets
  • regression of model parameters
  • comparison of models with each othe

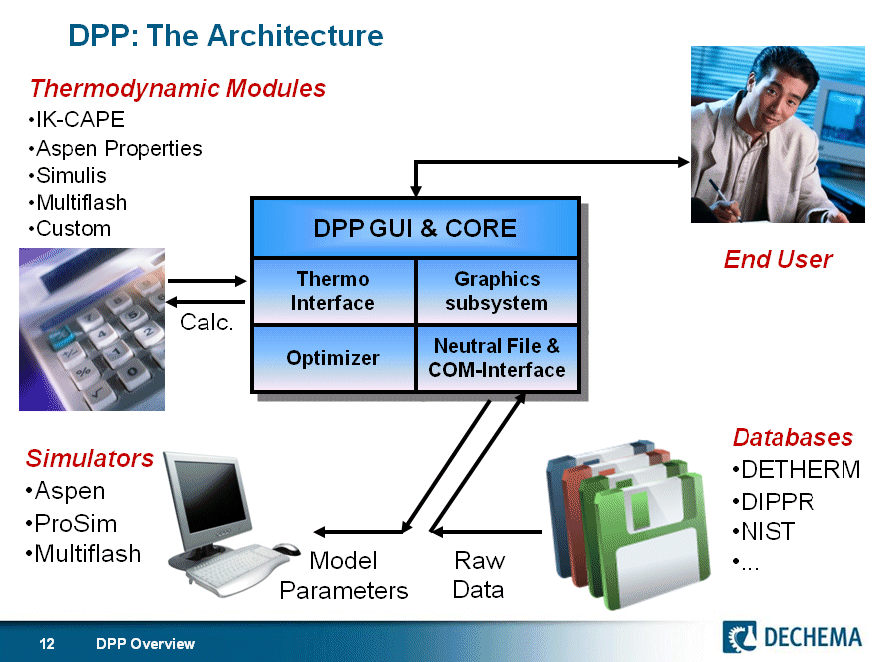
Architecture

dpp-overview

The main components of DPP are

  • GUI & CORE : The GUI is the glue between the end user and the system itself. The GUI is optimized for the representation of models and related raw data sets. The DPP CORE instead manages the information transfer between the different main components listed beneath.
  • Graphics Subsystem : It allows graphical representation of measured raw data and also model derived data in varitey of different plots.
  • N eutral File Interface : It is able to read and write raw thermophysical data and model parameters in the neutral IK-CAPE PPDX format. Data from a varitey of databases can be read in therefore. The regressed model parameters can also be loaded from a variety of process simulation packages.
  • THERMO interface : The DPP core does not contain a thermodynamics module inside. Instead any thermodynamics module having an open interface can be used in cooperation with DPP. Currently interfaces to Aspen Properties and the IK-CAPE thermodynamics are available.
  • Optimizer : The optimizer is the backbone of the DPP system.

The Optimizer

The optimizer is able to calculate a common objective value over n sets of data grouped in m blocks . For each of the m blocks a seperate objective and also error function can be used. To minimize the calculated objective value, the model parameters will be varied. This approach enables the DPP system to correlate simultaneous different data types using different error functions (e.g. to correlate VLE, LLE, HE, gammy infinity and azeotropic data all together). In each case the approach can be combined with a Maximum-Likelihood Algorithm for generation of the "true" values.

Featured algorithms Featured error functions
  • Simplex-Nelder-Mead
  • Powell
  • Broyden-Fletcher-Goldfarb-Shanno
  • modified Gauß-Newton
  • Least-Squares
  • Chi-Square
  • Absolut
  • Robust (based on Cauchy or Lorentzian error distribution )

Further Informationen

Further information on the Data Preparation Package DPP as well as prices you can request here .